Библиотека генерации случайной величины по закону Фишера

Описание: Код для выполнения генерации распределния случайных чисел по закону распределения Фишера.

Данная статья посвящена разбору алгоритма и кода для построяения случайных велечин с законом Фишера, а также построение графиков на их основе. Начнёмс…

Цель. Реализовать на ЭВМ и исследовать на точность алгоритм моделирования непрерывной случайной величины, распределенной по закону Фишера (число успехов в испытаниях), методом суммирования:

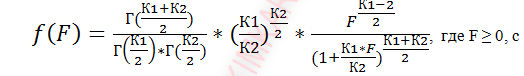
числом степеней свободы К1 и К2.

Математическое ожидание и дисперсия СВ, распределенной по закону Фишера, имеют вид:

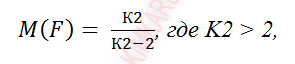
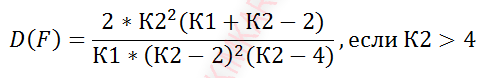
Для моделирования непрерывной случайной величины, распределенной по закону Фишера, использовалась следующая формула

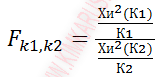
, с числом степеней свободы К1 и К2.
 Чтобы смоделировать одну случайную велечину необходимо пройти через алгоритм (рис. 1). Затем приступим к написанию кода

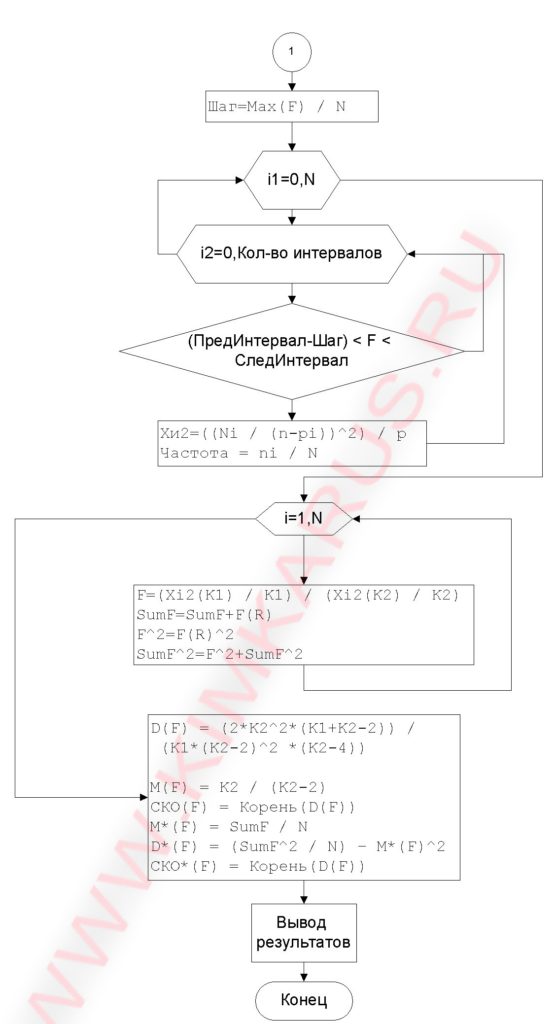
Допустим, у нас есть проект в Visual Studio и мы создали класс «Exp.cs», который содержит довольно простой код (Листинг 1):

public class Fisher
    {
        private Распределения.EnterValues enVal;
        private Распределения.OutValues ouVal;
        private Распределения.Xi_two Xi2_1;
        private Распределения.Xi_two Xi2_2;
        public Fisher(Распределения.EnterValues enVal, Распределения.OutValues ouVal, Распределения.Xi_two Xi2_1, Распределения.Xi_two Xi2_2)
        {
            this.enVal = enVal;
            this.ouVal = ouVal;
            this.Xi2_1 = Xi2_1;
            this.Xi2_2 = Xi2_2;
        }
        public void generate()
        {
            ouVal._arX = new double[enVal._N];
            enVal._MatO_T = 0.0f;
            enVal._Sko_T = 1.0f;
            ouVal._NameOfR = "Распределение Фишера";
            for (int i = 0; i < enVal._N; i++)
            {
                ouVal._arX[i] = genX(enVal._K1, enVal._K2, enVal._MatO_T, enVal._Sko_T);
            }
        }
        private double genX(int K1, int K2, float MatO, float Sko)
        {
            double Xi2_K1 = 0.0;
            double Xi2_K2 = 0.0;
            double x = 0.0;
            Xi2_K1 = Xi2_1.genX(MatO, Sko, K1);
            Xi2_K2 = Xi2_2.genX(MatO, Sko, K2);
            x = (Xi2_K1 / (double)enVal._K1) / (Xi2_K2 / (double)enVal._K2);
            return x;
        }
    }

Даю пояснения к листингу 1.

Здесь применяется подход из ряда статей «Распределения — (первая статья)«, т.е. имеется ввиду, что мы используем некий класс входных переменных(enVal) и выводимых(ouVal). В классе «ouVal» мы используем переменную для храненя случайных велечин (СВ) с экспоненциальным законом распредления «ouVal._arX[i]», куда мы записываем новые СВ. Входной параметр «enVal._Lya» является неотъемлемой частью этого закона распределния, а папраметр «enVal._N» означает количество генерирумых СВ.

Также, если вы используете «все в одном», то можно написать примерно следующимм кодом — Листинг 2.

Надеюсь, что вы имеете небольшое предстваления, как использовать эти листинги для своих целей.

Если все правильно сделать, то программа способна отображать графики и расчитывать величины правильно. Некоторые возможности представлены на рисунках ниже.

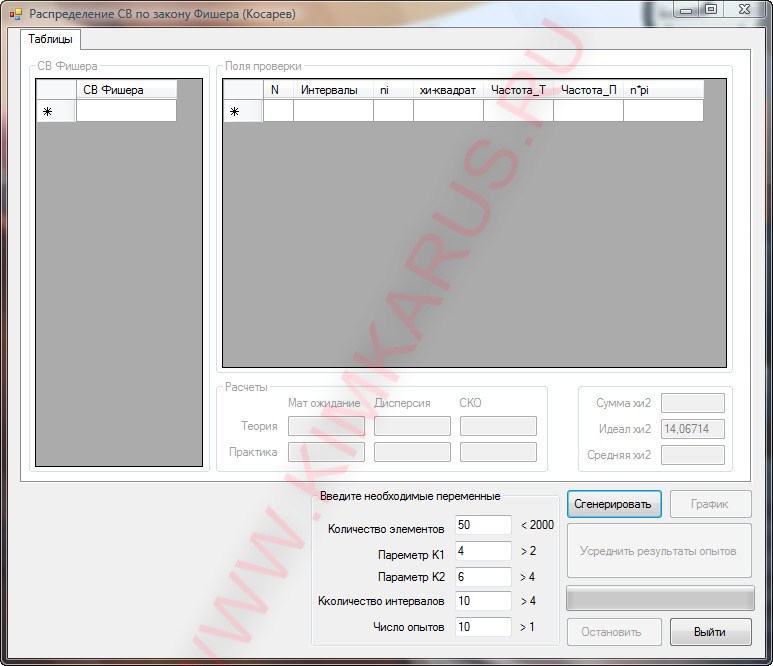
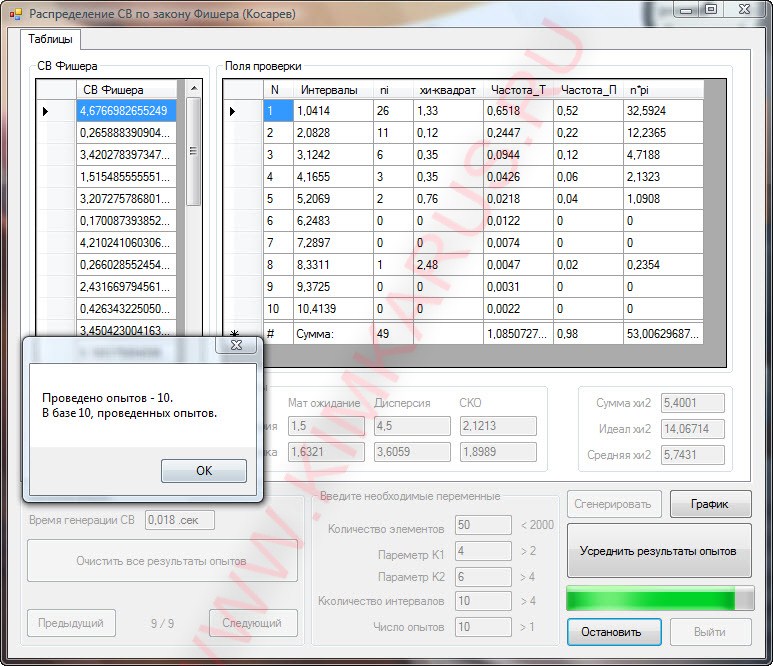
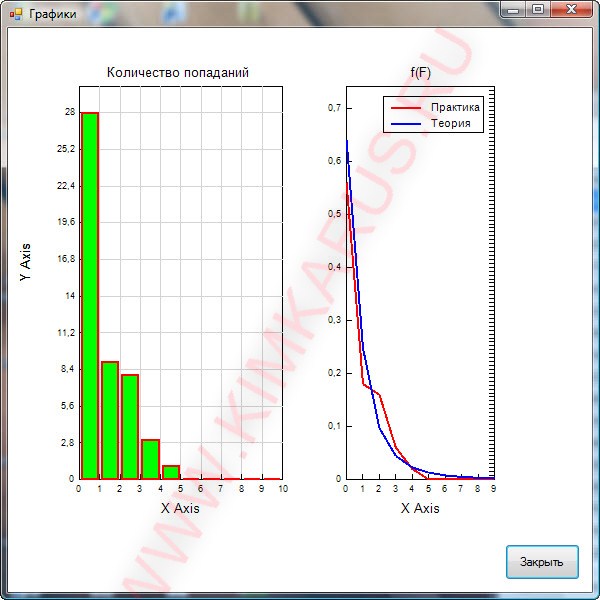
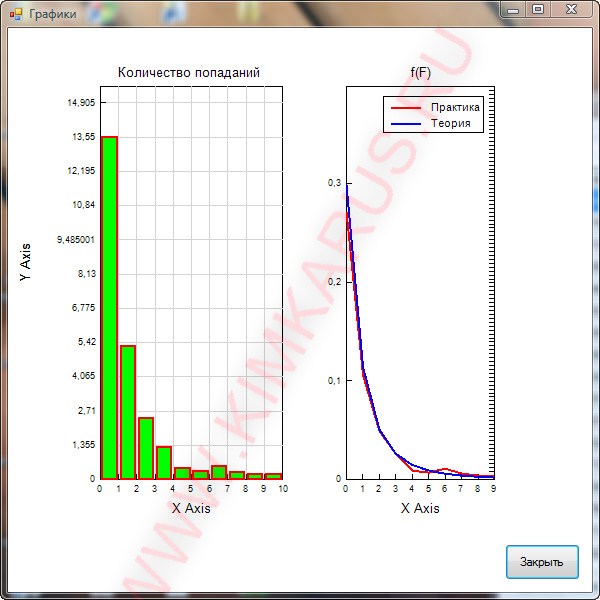
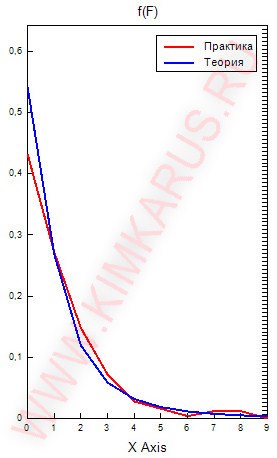
Хорошего дня.